skip to main |
skip to sidebar
Just returned from a timely conference. We spent a whole day discussing Common Core Math and sequencing learning for children in elementary mathematics instruction. One issue being discussed caught my attention since it has been a thorny, ongoing "problem" at our school. Subtraction with re-grouping. Need I say more? Second grade teachers would teach it. Students wouldn't be able to do it in third grade. Third grade teachers would teach it. Students wouldn't be able to do it. Fourth grade teachers would teach it and so on.
What is going on here? Why weren't our children learning to subtract? The concept didn't seem that difficult. The regrouping seemed insurmountable. What's up?
One thing suggested was that first grade teachers not teach double digit subraction at all. Leave subtraction to second grade. That way, students can start with an understanding that students are taking a group away from another group. Their strategy was to circle the top number, regroup every column where needed and then subtract (at this point, students can move left to right or right to left).
Also important was the use of counter, or manipulatives to reinforce the concept of subtaction and place value. This makes sense and hopefully will avoid students subtracting the smaller number from the larger number, no matter where is lies.
So, first grade teachers, Just Don't Do It!
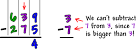
Today was "kick-off" day for fractions. Yahoo! It is probably one of my favorite days in math since I know we are embarking on a six to eight week trip learning all there is to know (in third grade) about fractions. We start off with a bang - that is ... a chocolate bang.
I pass out a notecard to each student. I show them a stack of Hershey's candy bars and tell them they get to "order" the size they want. They get very excited and the anticipation is like static electricity. They can almost taste the chocolate already! This is a rare treat since I don't believe in giving students any kind of candy as a reward. However, the benefits of this one activity outweigh the cons.
I write two fractions on the board- 1/12 and 1/4. I tell them they must write one down without sharing with their neighbor. Hersheys are already divided into 12 mini squares, or you can break them into 4 larger squares. I go around the room and hold up each piece requested before I set them on the card and read off the fraction.
When the realization hits, there are many ohhhs and ahhhs. Some students are grinning and some look quite unhappy. As they eat, we talk about what 1/12 and 1/4 mean as far as the numerator and the denominator. We also talk about the fact that fractions are kind of backwards, the larger the denominator, the smaller the fraction, or piece is. This is an experience we will refer back to over the next six to eight weeks.
We began a discussion about 1/3 and 1/6. When talking about the size of each piece, a student became confused. Another another student suddenly chirped, "Well, would you rather have a piece of candy bar cut into three pieces, or one cut into six pieces?" Suddely everyone nodded in agreement.
Materials I will be using to teach and assess this unit:Fraction Frenzy and 3rd Grade Common Core Fractions Assessment
Premade Blog Design by Delicious Design Studio


